Procesos lingüísticos:

Para facilitar la comprensión, elaboración y resolución de un problema, requerimos de la comprensión de la consigna y una serie de procedimientos lingüísticos para acceder al resultado. En el caso de la alumna, se observan que confunde las operaciones ante una situación problemática, de un enunciado verbal de suma.



Identificación de los superesquemas que necesita activar para resolver los problemas presentados y la necesidad de la reescritura desde el punto de vista lingüístico.


El primer problema requiere la activación del superesquema de cambio, ya que se modifican los conjuntos iniciales de ambos, a través de procedimiento de adicción y de sustracción.

• Situación problemática 1:
  
  
  En el cumpleaños de Marcos, regala los mismos caramelos a sus amigos. Tu ya tienes 10 caramelos, que te habían comprado tus padres. Cuando Marcos reparte los suyos, tienes 17. ¿Cuántos cramelos ha repartido Marcos a cada niño ?
  
  Superesquema de cambio.
  
  N. necesitaría activar un superesquema de cambio, el conjunto inicial (10) y el conjunto final (17)
  Se podría realizar una escenificación de la situación problemática y posteriormente una reescritura de los pasos dados.
  
  El segundo problema necesita del superesquema más que/menos, ya que éste nos plantea una disyuntiva en términos de comparación, a partir de una diferencia entre dos conjuntos. Pero antes deberemos aplicar un superesquema de cambio, para valorar con exactitud la cantidad de libros que posee cada conjunto (mayor y menor).
  
  
• Situación problemática 2.
  
  
  El padre tiene 20 libros y compra 12 mas. La madre tiene 15 y le regalan 10. ¿Quién de los dos tendrá más libros?
  
  Superesquema de cambio a.
  
  
  N., podría activar un superesquema de cambio para la situación del padre y otro para la madre.
  A partir de allí puede resolver la pregunta, haciendo una comparación ¿quién tiene más libros?
  
  Superesquema de cambio b.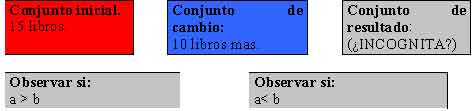
  
  Reescribir las dos situaciones problemáticas puede ayudar a resolver la pregunta.
  
  
• Situación problemática 3.
  
  En una canasta hay 30 naranjas. Juan agarra 10 y yo 5. ¿Cuántas naranjas quedan en la canasta?
  
  Superesquema Parte / todo.
  
  
  Superesquema de cambio.
  
  
  N., tendría que activar un superesquema parte/todo.
  
  Por un lado, en el conjunto parte 1, es el número de naranjas que agarra Juan.
  En el conjunto parte 2, es el número de naranjas que agarro yo.
  El conjunto total es la suma de las dos cantidades, es decir: la incógnita.
  
  Luego, se tendría que activar un superesquema de cambio en el que se encuentran que el conjunto inicial estarían las 30 naranjas de la canasta y el conjunto de cambio es el resultado del paso anterior y el conjunto resultado es la incógnita
  
  
• Situación problemática 4.
  Dos amigos juntan sus chapitas para jugar. Uno tiene 30 y el otro tiene 12. ¿cuántos tienen entre los dos?
  
  Superesquema parte / todo.
  
  
  N., tendría que activar un superesquema parte / todo, en el que en el conjunto parte 1 estarían las chapas de un amigo y en el conjunto parte 2, las chapas del otro amigo.
  El conjunto total: es la incógnita.
  
  Página anterior
  Página siguiente

ARTÍCULOS RELACIONADOS

• ¿Cura la Música? (Parte I)
• ¿Cura la Música? (Parte III)
• Nunca es Triste la Verdad solamente es IRREDUCTIBLE. (Parte II)
• Nunca es Triste la Verdad solamente es IRREDUCTIBLE. (Parte I)
• Personalizar la educación, una necesidad actual. (Parte III)
• Personalizar la educación, una necesidad actual. (Parte II)
• Personalizar la educación, una necesidad actual. (Parte I)
• Nunca es Triste la Verdad solamente es IRREDUCTIBLE. (Parte III)
• Trayectos pre Profesionales (TpP). (Parte IV)

OTROS TEMAS

Encuesta